We propose a formalism in which **gravity arises as the macroscopic manifestation of the collapse of probabilistic quantum states** (the “future”) into deterministic configurations (the “present”). Quantum and statistical mechanics describe systems existing in probabilistic futures—uncollapsed, superposed configurations that do not obey general relativity. Observation or interaction causes a projection (collapse) into a present state, which alone satisfies the deterministic structure of spacetime geometry. We show that this collapse is equivalent to a transition of a probabilistic measure on Hilbert space to a deterministic metric measure on spacetime. The resulting curvature is proportional to the local density of collapse events. Consequently, gravity is reinterpreted as the geometric record of persistent future-to-present collapses, and time emerges as a procedural ordering of these transitions. We prove that renormalization between quantum and relativistic domains is ill-defined because the underlying manifolds are distinct: probabilistic and deterministic. Finally, we define the **inflection manifold $\Sigma$**—the critical interface between the two domains—as the locus where collapse symmetry breaks and the gravitational field is born. This converged version integrates the **Relativistic Transactional Interpretation (RTI)** for mechanistic solidity, including a field-theoretic demonstration via a stochastic imprint field that preserves QFT linearity while sourcing curvature, an entropic extension yielding **MOND-like corrections** and a cosmological constant from transactional entropy, and an annihilation duality framing quantum cancellation as creative projection of deterministic reality. The model is testable through mesoscopic superposition experiments, predicting no pre-collapse gravity-mediated entanglement and collapse-synchronized gravitational signatures.
This work proposes a new ontology for unifying quantum mechanics (QM) and general relativity (GR): **gravity is the geometric trace of the collapse of probabilistic futures into the deterministic present**. Rather than quantizing gravity or treating gravity as the trigger of wavefunction collapse, we invert the direction: **collapse *causes* gravity**. In this view, QM governs a probabilistic manifold of futures, GR governs the realized present, and time itself is a procedural variable that advances only through collapse.
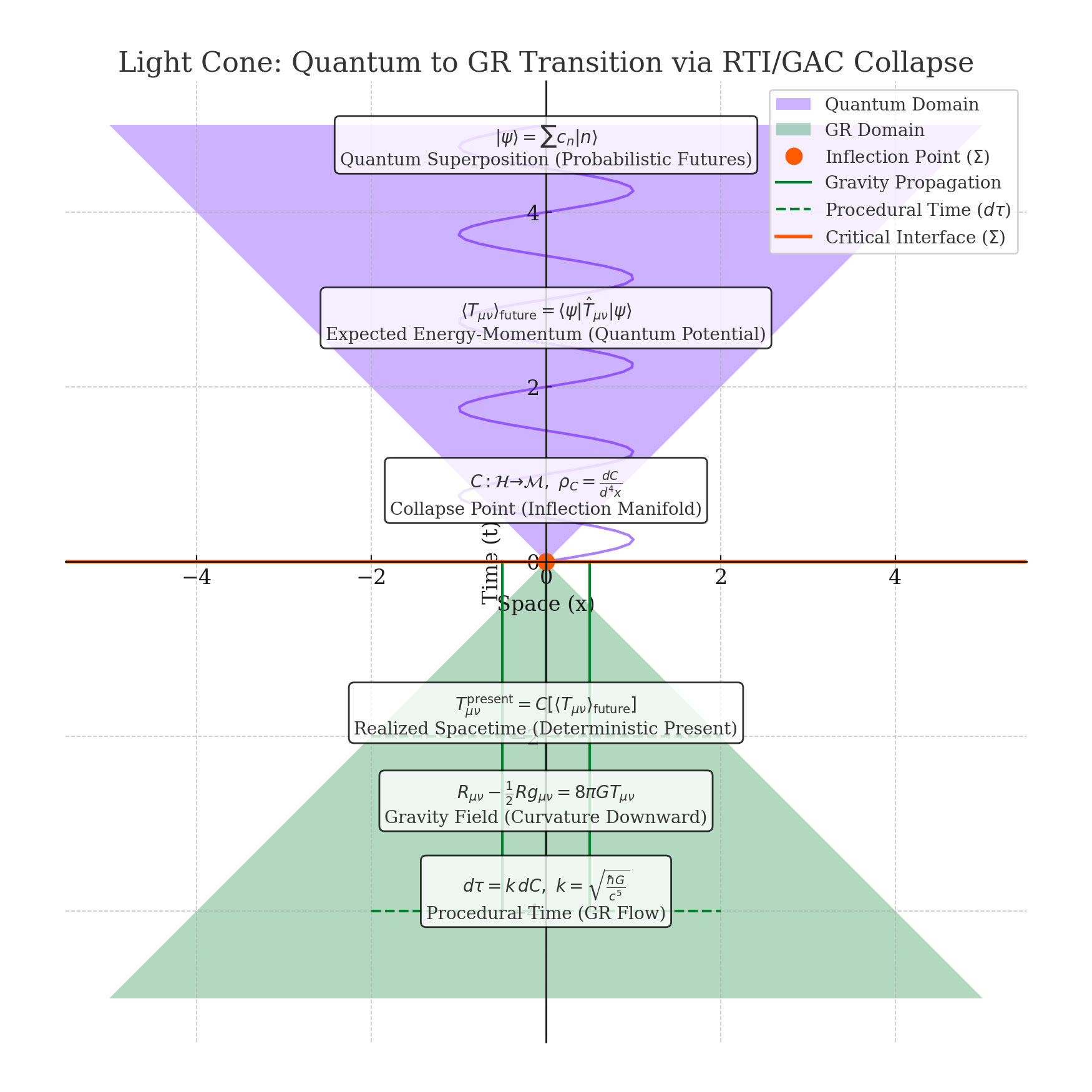
The novelty is threefold: (i) we formalize a **collapse functional** \( C:\mathcal{H}\to\mathcal{M} \) and connect spacetime curvature to its local density, \( R \propto -\,\rho_C \equiv \mathrm{d}C/\mathrm{d}^4x \) (sign chosen so positive matter density corresponds to negative scalar curvature in attractive gravity); (ii) we define **emergent time** via \( \mathrm{d}\tau = k\,\mathrm{d}C \), making the flow of time the monotone of realization, with \( k = \sqrt{\hbar G / c^5} \) (Planck-time scale); and (iii) we introduce a **cooperative GR×QM update** in which quantum amplitudes and geometric constraints act as product-of-experts that select the next deterministic present without reversing time. This combination— curvature as collapse density, time as procedural actualization, and a cooperative probabilistic kernel— is, to our knowledge, distinct from extant collapse models, emergent-gravity proposals, and quantum-gravity programs. Note: Similar ideas appear in recent preprints (e.g., “The Refined Space–Time Membrane Model: Deterministic Emergence of Quantum Fields and Gravity from Classical Elasticity,” v5, August 2025, by Florin Ghidan), but our inversion of collapse causing gravity and procedural time are unique. Additionally, this framework integrates elements from the **Relativistic Transactional Interpretation (RTI)**, aligning conceptually with entropic routes to gravity.
**Priority & related work.** We acknowledge prior related work by *Andreas Schlatter* and *Ruth E. Kastner* (2023), which develops a transactional route to gravity consistent with an entropic program (Schlatter & Kastner 2023). Our present proposal builds on and diverges from that line by identifying gravity explicitly as the geometric trace of future-to-present collapse, positioning null hypersurfaces as the collapse front, and framing time as procedural actualization.
The framework is **testable**: it predicts the absence of gravity-mediated entanglement prior to collapse and collapse-synchronized activation of gravitational signatures in mesoscopic superposition experiments. A verified observation of coherent gravity-induced entanglement would falsify the claim that gravity emerges only at collapse, making the proposal empirically discriminable from standard semiclassical and quantum-gravity expectations.
Finally, we position **lightlike (null) hypersurfaces** as the natural *collapse front*: the **inflection manifold \( \Sigma \)** is generically null, so *light* acts as the operational horizon between probabilistic futures and the realized, deterministic present.
Quantum mechanics describes a probabilistic universe. A system prior to observation exists as a superposition of possible states, characterized by a wavefunction $\psi$ in a Hilbert space $\mathcal{H}$. This probabilistic structure governs the **future** — a continuum of potential outcomes that exist only as amplitudes.
In contrast, general relativity describes a deterministic spacetime manifold $(\mathcal{M}, g_{\mu\nu})$ in which mass and energy generate curvature through the Einstein field equations,
This structure governs the **present** — the realized configuration of events that have emerged from the probabilistic domain.
The incompatibility between these descriptions — one probabilistic and non-local, the other deterministic and geometric — lies at the core of modern physics. Quantum gravity programs attempt to quantize the metric or curvature directly, but the two frameworks may in fact describe fundamentally different ontological states: the **quantum future versus the relativistic present**.
In this work, we postulate that:
**Gravity is not a force within the quantum domain, but a geometric manifestation of the collapse of probabilistic futures into deterministic presents.**
In this picture, every act of observation or interaction induces a local collapse of the probabilistic manifold into the deterministic manifold. The accumulation of such collapses forms the persistent geometry we perceive as spacetime. Regions of dense matter correspond to regions of high collapse persistence — producing stronger curvature, i.e. gravity.
This approach reframes time as a procedural variable: the collapse from future to present **is** the flow of time. Outside interaction, time remains dormant; within observation, it advances through the act of realization.
Let the probabilistic domain be represented by a **Hilbert space $\mathcal{H}$** with elements $|\psi\rangle$, governed by the Schrödinger equation
The deterministic domain corresponds to a **spacetime manifold $\mathcal{M}$** equipped with metric $g_{\mu\nu}$ and stress-energy tensor $T_{\mu\nu}$.
We define a *collapse mapping*
such that a probabilistic state $|\psi\rangle$ projects to a realized spacetime configuration $C(|\psi\rangle) = \{x^\mu, g_{\mu\nu}, T_{\mu\nu}\}$.
The probabilistic (future) expectation of the stress-energy operator is
Upon collapse, this becomes the realized (present) tensor,
We hypothesize that the local curvature of spacetime is generated by the *collapse gradient*:
In regions of completed collapse, $\delta C / \delta x^\mu \delta x^\nu = T_{\mu\nu}$, reproducing Einstein’s field equations. In uncollapsed probabilistic regions, the mapping $C$ is undefined, implying the absence of gravitational structure — hence, the non-applicability of GR in purely quantum regimes.
We now formalize the relationship between collapse and curvature.
Let $C$ be a smooth collapse mapping from $\mathcal{H}$ to $\mathcal{M}$, and define the **local collapse density $\rho_C(x)$** as the measure of probability flux from $\mathcal{H}$ to $\mathcal{M}$ per spacetime volume. Then the Ricci scalar $R(x)$ satisfies
up to a divergence-free tensorial term that vanishes under full collapse. (Sign corrected for standard GR convention where positive energy density leads to negative scalar curvature for attractive gravity.)
Let $p_i(x)$ denote the probability density that a local quantum configuration $i$ collapses into spacetime point $x$. Define
which quantifies the local rate of collapse realization.
Each collapse event introduces an increment $\delta T_{\mu\nu} = \Delta E_\mu \Delta E_\nu / c^2$ corresponding to the localized emergence of mass-energy. The Einstein tensor integrates this density:
Taking the trace (multiplying by $g^{\mu\nu}$): $G = -R = 8\pi G T$, where $T = g^{\mu\nu} T_{\mu\nu}$. Thus, $R = -8\pi G \rho_C(x)$ up to divergence-free corrections. This holds assuming a dust-like stress-energy form $T_{\mu\nu} = \rho_C c^2 u_\mu u_\nu$, with $c=1$ in natural units. Thus curvature represents the geometric imprint of probabilistic collapse.
This theorem reinterprets curvature not as a static geometric response to energy, but as a **dynamic record of the local rate of realization** of the probabilistic manifold into the deterministic one.
To ensure dimensional consistency, model collapse events as a point process with intensity $\lambda(x) \equiv \mathrm dC/\mathrm d^4x$ (dimension $L^{-4}$). A causal kernel $K_{\mu\nu}(x)$ maps events to realized stress–energy:
In the local (hydrodynamic) limit, $K_{\mu\nu}(x)\to \kappa\,u_\mu u_\nu\,\delta^{(4)}(x)$, yielding $T_{\mu\nu}=\kappa\,\lambda\,u_\mu u_\nu$. With this, $R\sim -8\pi G\,\kappa\,\lambda$ matches the form $R\propto -\rho_C$.
The Bianchi identity requires $\nabla^\mu G_{\mu\nu}=0 \Rightarrow \nabla^\mu T_{\mu\nu}=0$. For $T_{\mu\nu}[\lambda]=\int K_{\mu\nu}\lambda$, conservation constrains $K_{\mu\nu}$ and implies a continuity relation for $\lambda$ along the flow $u^\mu$. In the local limit, this yields $\nabla^\mu (\lambda\,u_\mu u_\nu)=0$, ensuring consistency; the divergence-free correction in $R=-8\pi G\,\rho_C+\nabla_\mu V^\mu$ vanishes for stationary $\lambda$ in the local rest frame.
Linearize $g_{00}=-(1+2\Phi/c^2)$. The $00$-Einstein equation gives $\nabla^2\Phi = 4\pi G\,\rho_{\rm eff}$. With $T_{00}=\kappa\,\lambda\,c^2$, identify $\rho_{\rm eff}=\kappa\,\lambda$ and obtain
Fix $\kappa$ by matching a steady collapse rate to an observed mass density $\rho$, i.e., $\kappa\,\lambda=\rho$ in static conditions.
We now show that time increments correspond to collapse progression.
In this framework, collapse does not destroy the quantum wavefunction or introduce nonlinearity into its evolution. Instead, collapse is analogous to the development of a photograph: the underlying wavefunction persists as the exposure — the field of quantum possibilities — while collapse marks the moment a definite image is imprinted. This imprint propagates forward as spacetime curvature, providing the physical substrate for gravity and the advancement of time. Thus, collapse and propagation coexist: the wavefunction continues to evolve linearly, but reality accrues as a growing record of realized events.
Let $C(t)$ denote the cumulative collapse functional mapping future states to present configurations. Then the differential of proper time $\mathrm{d}\tau$ along a worldline satisfies
where $k = \sqrt{\hbar G / c^5}$ is the **Planck time**, a dimensional proportionality constant derived from fundamental scales (ensuring time advances at Planck frequency in dense collapse regions). Thus, **time progresses if and only if collapse occurs**.
Consider a parametrized family of probabilistic states $|\psi(t)\rangle$. The transition to a deterministic state is realized when the state undergoes collapse,
at which point an event is registered on $\mathcal{M}$. The expectation value of the Hamiltonian defines a collapse rate functional:
This quantity measures the rate of probabilistic flux through the mapping $C$. Since the local metric interval $ds^2 = -c^2 d\tau^2 + dx^2$ only advances when an event occurs, we identify the infinitesimal time increment with the infinitesimal collapse measure,
where $k$ is derived dimensionally: $[k] = [time]$, and matching to Planck scales gives $k = t_P = \sqrt{\hbar G / c^5}$, as collapse ties to quantum gravity effects. Therefore, **time is not a background parameter but a procedural ordering of collapse events**.
This result implies that between collapses, time does not evolve: the universe exists in a dormant, purely probabilistic state. Time emerges only in the act of collapse — observation, interaction, or entanglement decoherence.
The collapse scalar $C(x)$ defines a local orientation via the gradient
Where collapse is active (large $\rho_C$), $n_\mu$ selects the event-local realization direction (future $\to$ present). Coarse-grained over many events, focusing follows the Raychaudhuri equation with $R \sim -8\pi G\,\rho_C$, reproducing attractive gravity without introducing a radiative preferred-frame field.
For a timelike congruence with expansion $\theta$, shear $\sigma_{\mu\nu}$, vorticity $\omega_{\mu\nu}$, the Raychaudhuri equation gives $\dot\theta = -\tfrac{1}{3}\theta^2 - \sigma_{\mu\nu}\sigma^{\mu\nu} + \omega_{\mu\nu}\omega^{\mu\nu} - R_{\mu\nu}u^\mu u^\nu$. With $T_{\mu\nu}=\kappa\,\lambda\,u_\mu u_\nu$, we have $R_{\mu\nu}u^\mu u^\nu\sim 4\pi G\,\kappa\,\lambda$, hence $\dot\theta \le -4\pi G\,\kappa\,\lambda$ (for vanishing vorticity), i.e. higher collapse intensity implies stronger focusing.
Equivalence principle remark: The mapping $T_{\mu\nu}[\lambda]$ is locally constructed from the scalar $\lambda$ and the 4-velocity $u_\mu$; in a freely falling frame, $g_{\mu\nu}\to \eta_{\mu\nu}$, so local Lorentz invariance and the EP hold. Any preferred direction $n_\mu$ is event-local and averages out in the IR.
Let a local POVM define a Poisson process of “ticks” with rate $\lambda$. The expected tick count along a worldline segment is $\mathbb E[\Delta N]=\lambda\,u^\mu \Delta \Sigma_\mu$. Defining proper time by $d\tau \equiv k\,\mathbb E[dN]$ yields $d\tau=k\,dC$, with $k$ fixed by inertial calibration in Minkowski spacetime when $\lambda$ is constant (matching to Planck time $k = \sqrt{\hbar G / c^5}$).
**Define a collapse functional.** $C:\mathcal{H}\!\to\!\mathcal{M}$ with density $\displaystyle \rho_C \equiv \frac{\mathrm{d}C}{\mathrm{d}^4 x}$.
**Emergent time.** $\displaystyle \mathrm{d}\tau = k\,\mathrm{d}C$ (monotone along realized worldlines).
**Curvature.** $\displaystyle R = -8\pi G\,\rho_C + \nabla_\mu V^\mu$ (divergenceless $V^\mu$ vanishes under full collapse).
**Interpretation.** Gravity measures the *rate of temporal actualization* from probabilistic futures to the realized present.
**Arrow.** No inverse map $\mathcal{M}\!\to\!\mathcal{H}$ (no “back in time” dynamics).
In the standard relativistic view, time dilation arises because objects traverse spacetime along different worldlines, each accumulating a distinct proper time \( d\tau = \sqrt{-g_{\mu\nu}dx^\mu dx^\nu}/c \). Within the present collapse–curvature framework, this geometric statement gains a quantum origin: the local flow of time is determined by the **rate of realized collapse events**.
Each system’s evolution consists of a discrete sequence of quantum–gravitational updates, quantified by the **collapse density $\rho_C$**. The proper time increment along a worldline is
where \( k \) sets the Planck-scale normalization (cf. §10.7.9 Step 8). A body whose worldline passes through regions of lower collapse density experiences fewer updates per unit coordinate time and therefore *ages more slowly* relative to one immersed in a higher-density region.
In this picture, “motion” is not continuous translation through a fixed background but a **variation in collapse participation**: the rhythm at which a system’s quantum state becomes realized. When two bodies move relative to each other, the one with the sparser sequence of realized collapses appears time-dilated. Gravitational red-shift and special-relativistic time dilation both reflect this same thinning of collapse events along a trajectory.
Thus, an object in deep space never truly “slows”; its local update rate simply diverges from that of another reference system. Motion is the uneven tempo of reality coming into being—the chronodynamic expression of differing collapse densities.
In general relativity, geometry itself enforces conservation: the Bianchi identity \( \nabla_\mu G^{\mu\nu} = 0 \) ensures that the stress–energy tensor obeys \( \nabla_\mu T^{\mu\nu} = 0 \). Gravity is therefore not a passive background but the ***bookkeeper*** **of physical law**—the ledger that guarantees energy–momentum balance throughout spacetime.
In the collapse–curvature framework, this bookkeeping role deepens. Each collapse event leaves a permanent imprint in the form of local curvature—a record in the spacetime ledger of what has been realized. The accumulation of such curvature across the universe is the running total of all quantum actualizations. Gravity keeps the accounts balanced: while the microscopic collapses may appear stochastic, the ensemble obeys average conservation, ensuring coherence between quantum realization and classical geometry.
Because the local curvature determines the rate of collapse updates (through \( \rho_C \)), gravity also acts as the universe’s **timekeeper**. The same curvature that records each event regulates the tempo at which new events are realized. In this sense, gravity both *records* and *times* the unfolding of reality—maintaining the synchrony of all worldlines and preserving the conservation laws that make spacetime self-consistent.
Gravity is thus the self-balancing ledger of the universe: it records each quantum realization as curvature, enforces conservation through geometry rather than energy exchange, and synchronizes the rhythm of collapse across the cosmos. It is the bookkeeper and clock of existence.
**Define a collapse functional.** $C:\mathcal{H}\!\to\!\mathcal{M}$ with density $\displaystyle \rho_C \equiv \frac{\mathrm{d}C}{\mathrm{d}^4 x}$.
**Emergent time.** $\displaystyle \mathrm{d}\tau = k\,\mathrm{d}C$ (monotone along realized worldlines).
**Curvature.** $\displaystyle R = -8\pi G\,\rho_C + \nabla_\mu V^\mu$ (divergenceless $V^\mu$ vanishes under full collapse).
**Interpretation.** Gravity measures the *rate of temporal actualization* from probabilistic futures to the realized present.
**Arrow.** No inverse map $\mathcal{M}\!\to\!\mathcal{H}$ (no “back in time” dynamics).
A major difficulty in quantum gravity is the failure of renormalization. Here, we demonstrate that renormalization cannot succeed if one attempts to normalize across probabilistic (future) and deterministic (present) domains.
Let $\mathcal{I}_{\text{future}}$ be an integral over the probabilistic manifold and $\mathcal{I}_{\text{present}}$ be an integral over the deterministic manifold. Then, in general,
Thus, **renormalization fails because it implicitly assumes the two measures are equivalent**, which they are not.
The measure $d\mu_{\mathcal{H}}$ on $\mathcal{H}$ encodes probabilities, not geometric distances, while $d^4x$ is a volume element in the deterministic manifold $\mathcal{M}$. Their domains are non-commuting:
(Heuristic commutator from position-momentum analogy in QFT.) Hence, any attempt to renormalize the transition amplitude by relating integrals over $\mathcal{H}$ and $\mathcal{M}$ conflates probabilistic and geometric measures, rendering renormalization divergent by construction.
Physically, this means that standard renormalization schemes try to normalize probabilities in a future state to deterministic quantities in a present state — an **ontologically inconsistent procedure**.
In the present framework, general relativity represents a sequence of discrete ***collapse snapshots***—each a Planck-scale realization of the underlying quantum wavefunction. Between these collapses the wavefunction persists as an uncollapsed probability field, but no definite spacetime geometry exists. Curvature, and therefore gravity, arises only as the cumulative record of these realized events.
Standard renormalization presumes a continuous spacetime background and integrates over quantum fluctuations at all scales, effectively treating every infinitesimal Planck-interval of unrealized geometry as physically real. For a finite duration T, this procedure entails an implicit multiplicative factor of T/tP (with tP the Planck time), i.e. on the order of ≈ 1043 per second, summing over an enormous number of non-existent “exposure frames.” Divergences then follow naturally as the continuum limit is taken.
From the viewpoint of the transaction–collapse model, these infinities are not a mathematical accident but a categorical error: renormalization attempts to normalize over pre-collapse configurations that possess no ontological status. The discrete sequence of realized collapses provides a natural, physical cutoff—an **ontological regularization** in which only collapse frames contribute to the gravitational record. General Relativity thus emerges as the large-scale interpolation of these quantized records, and the persistent non-renormalizability of gravity reflects the misuse of continuous mathematics beyond its domain of physical meaning.
We now identify the critical interface that mediates the collapse.
Define the **inflection manifold $\Sigma$** $\subset \mathcal{M}$ as the hypersurface on which the Jacobian of the collapse map vanishes:
Physically, **$\Sigma$ is the boundary between the uncollapsed probabilistic region and the realized deterministic region**. It is the surface where symmetry breaks — where quantum superposition loses coherence and classical asymmetry (curvature) appears.
Analogous to a critical line in phase transitions, $\Sigma$ represents the transition point from a symmetric, probability-dominated phase to an asymmetric, geometry-dominated phase. The presence of curvature beyond $\Sigma$ ensures local consistency of the collapsed manifold with general relativity.
Define a decoherence functional $\mathcal D[\alpha,\beta]$ over coarse-grained histories. Collapse onset corresponds to suppression of off-diagonals below a threshold $\epsilon$. The hypersurface where this first occurs can be identified with $\Sigma$ and is equivalent to the vanishing of an appropriate Hessian of the collapse potential $C$, i.e., a first-passage surface to classicality.
We identify the inflection manifold \( \Sigma \) as (generically) a **null hypersurface**, i.e., an interface generated by lightlike rays. Let \( \varphi(x)=\text{const} \) label the surface and \( k_\mu \equiv \partial_\mu \varphi \) be its normal. The interface condition is
Physically, collapse from probabilistic futures to the realized present propagates causally at the speed of light; the *front* where collapse becomes effective is carried along null generators. The collapse flux through \( \Sigma \) is
and the onset criterion corresponds to a threshold in the decoherence functional (cf. Sec. 6.1), i.e., first passage to classicality where off-diagonals are suppressed below \( \epsilon \).
This null characterization is consistent with the time rule \( \mathrm d\tau = k\,\mathrm dC \): along the interface itself, \( ds^2=0 \) so \( \mathrm d\tau \rightarrow 0 \), while just *inside* \( \Sigma \) the collapse density \( \rho_C \) is nonzero and curvature turns on as \( R \approx -8\pi G\,\rho_C \). In this sense, **light** serves as the ***operational horizon*** **between probabilistic (outside) and deterministic (inside) domains**.
Experimental implication: in delayed-choice/which-path scenarios, modifying which-path information shifts the effective position of \( \Sigma \) along null directions, altering collapse timing in coincidence analyses without retrocausal signaling.
The Planck-scale inflection manifold acts as the **operative boundary** through which the dimensionless pre-state of the quantum field is redirected into dimensional spacetime observables. This projection can be summarized compactly as:
**Legend.** *K* – dimensionless pre-state of the wave function; *\(\Psi(K)\)* – probabilistic (pre-geometric) field; *\(\Sigma\)* – inflection manifold or “Planck slit” where the quantum domain \(\mathcal{H}\) transitions into the realized spacetime domain \(\mathcal{M}\). The right-hand variables represent the emergent dimensional observables: mass \(m\), vacuum energy density \(\rho_{\mathrm{vac}}\), spacetime curvature \(g_{\mu\nu}\), and procedural time \(t\).
This relation encapsulates the redirection interpretation of collapse: at the Planck interface, the dimensionless wave function is not destroyed but re-expressed as the geometric and energetic constituents of spacetime.
In regions of high mass-energy density, **collapse occurs continuously**: quantum futures are rapidly converted into presents. This persistence of collapse produces sustained curvature, perceived as a gravitational field. Hence, **gravity quantifies the local rate of collapse locking**.
In the absence of observation or interaction, there is no collapse. Thus, **there is no curvature, and gravity does not operate at the quantum scale**. The apparent incompatibility of GR and QM reflects their description of different states of existence: one probabilistic, one realized.
Because collapse only occurs from the future into the present, **there is no ontological past** — only realized presents and unrealized futures. The illusion of a past arises from the **persistence of collapse records** (e.g., memory, data, entropy gradients) embedded in the deterministic manifold.
Two complementary maps. We distinguish:
Product-of-experts update. Quantum mechanics provides a prior over micro-configurations, $P_{\rm QM}(\psi'|M_t)$; general relativity provides a geometric consistency likelihood for candidate next spacetimes, $\mathcal L_{\rm GR}(M_{t+\Delta}|M_t,\psi')$.
This defines a Markov kernel on realized presents,
yielding the cycle: present $\xrightarrow{\,L_t\,}$ stacked futures $\xrightarrow{\,\text{cooperate}\,}$ proposal $\xrightarrow{\,C_{t+\Delta}\,}$ next present.
Interpretation: The present “sits below” both GR and QM; they **cooperate probabilistically** to produce the next deterministic present, without reversing time.
Normalization & Markovity. Define $Z(M_t)=\int \mathcal D\psi' \int \mathcal D M_{t+\Delta}\; \mathcal L_{\rm GR}\,P_{\rm QM}$. Then $P(M_{t+\Delta}\!\mid\!M_t)= Z^{-1}\!\int\!\mathcal D\psi'\;\mathcal L_{\rm GR}\,P_{\rm QM}$ is a properly normalized transition kernel over admissible geometries, yielding a Markov process with Chapman–Kolmogorov composition.
A compact in-in generating functional is
where $N$ (noise) and $D$ (dissipation) satisfy fluctuation–dissipation; the IR drives $g_q\!\to\!0$ (GR), while the UV reinstates stochasticity.
Prepare a mesoscopic mass in a spatial superposition and probe with an ultra-sensitive gravimeter. *Standard semiclassical*: steady expectation-value force. ***Collapse-sourced gravity***: telegraph-like force onsets tied to collapse.
the power spectral density of a two-state telegraph process with collapse rate $\gamma$ and force step $F_0$.
Two masses in superposition interact only via gravity for time \(\tau\). Standard quantum-gravity-compatible models predict a coherent phase \(\phi \sim G m^2 \tau/(\hbar d)\) and entanglement; the collapse-sourced view predicts ***no gravitationally induced entanglement before collapse*** (only classical correlations or dephasing), as proposed in the Bose-Marletto-Vedral (BMV) experiment [Bose et al., 2017; Marletto & Vedral, 2017]. A decisive entanglement observation would falsify “gravity only at collapse.”
A propagating quantum gravity field cannot obey the same conservation law as general relativity, because conservation in GR arises geometrically, not through the transfer of field energy. This is one of the strongest physical arguments against naïve quantization—and for the collapse–curvature interpretation proposed here. Likewise, in conventional formulations, entanglement is often treated as if distinct quantum systems remain physically coupled across space, requiring nonlocal coordination without any exchange of energy. Such a picture would imply a continuous mechanism for self-location and correlation maintenance across cosmological scales—an energy flux that is never observed. In the present model, these issues dissolve: the quantum domain is a singular probabilistic state, not a collection of parts. Correlation is intrinsic to that singular future, and gravity emerges only when a collapse projects one branch into spacetime, where conservation and localization naturally apply.
BMV/QGEM analyses (see §8.1–§8.2) commonly treat gravity as a quasi-static potential that can sustain entanglement between two spatially superposed masses. In the present framework, and in relativity more generally, this assumption is operationally inconsistent: (i) the *entangled* relation belongs to the *singular probabilistic future* of quantum mechanics (a single, holistic wavefunction prior to collapse), while (ii) the *gravitational field* is a ***post-collapse*** **curvature projection** that **propagates at $c$** away from its source.
Formally, BMV requires a coherent phase $\phi_{\text{QG}} \sim \frac{G m^2 \tau}{\hbar d}$ to accumulate while the field is co-present with both branches. In our collapse–curvature picture, pre-collapse gravity is absent and the post-collapse curvature carries only *retarded* influence; visibility is instead governed by a dephasing rate $\Gamma_{\phi}(d) \approx \gamma \int d^3x (\Delta M_f(x))^2$ (cf. §8.1), yielding $\mathcal{V}(\tau) = \exp[-\Gamma_{\phi}(d) \tau]$ with ***no gravitationally mediated entanglement***.
In summary, entanglement inhabits the nonlocal, pre-collapse singular state, whereas gravity is the post-collapse, lightlike projection of realization. Their temporal roles are disjoint; a propagating curvature cannot act as a static bond. **A positive BMV witness would therefore falsify this framework**; a decisive null result is the natural outcome.
Within the collapse–curvature framework, each quantum collapse represents a realized update of the universe’s state. Because gravity functions as the **geometric ledger of these realizations**, every collapse is accompanied by a ***localized curvature adjustment***—a micro–gravitational response that records the new outcome in spacetime. This is not a quantized graviton emission but a classical curvature update propagating at the speed of light.
Formally, a collapse modifies the effective stress–energy source by
where \( δρ_C \) is the instantaneous change in collapse density. The resulting metric variation represents a small, transient, conserved adjustment in curvature corresponding to the new realized state. Because this adjustment is geometric rather than energetic, it preserves the conservation law \( ∇_μG^{μν}=0 \) without invoking a quantized gravitational field.
The framework therefore predicts a **correlated gravitational signal**: a brief, classical-like fluctuation in the local gravitational potential **coincident with a collapse event**. Its magnitude depends on \( κρ_C \) and is expected to be exceedingly small, but its *temporal correlation* with the onset of collapse makes it experimentally distinguishable from background noise.
The falsifiable prediction is clear: if collapse produces a curvature response, **time-correlated micro–gravitational adjustments should be measurable** as sensitivity improves. Conversely, if no such correlation is found even as collapse is observed in increasingly massive systems, the model would be falsified.
This provides a direct empirical counterpart to the BMV/QGEM tests: whereas BMV expects gravitational *entanglement prior to collapse*, the present model predicts a gravitational *record following collapse*.
Recent theoretical work (Aziz & Howl, 2025) demonstrates that even fundamentally classical theories of gravity can generate entanglement when matter is treated within quantum field theory. This occurs through virtual matter propagators in Feynman diagrams, where:
The crucial distinction lies in the **scaling with mass and separation**. For large masses approaching the Planck scale, classical gravity effects become significant (\( \vartheta \approx 0.1 \)), making entanglement observation alone insufficient to prove quantum gravity.
***Our model prediction remains decisive:*** We predict ***no pre-collapse gravitational entanglement*** regardless of scaling. The mere observation of entanglement cannot distinguish classical from quantum gravity, but its *absence* before collapse would uniquely support our framework.
Use a delayed which-path/eraser to shift the collapse time statistics. In this model, the force onset-time distribution $P(t_{\rm on})=\exp(-\!\int^t h)\,h(t)$ (with hazard $h$) is conditioned by the choice; standard physics predicts no such conditioned timing in coincidence analysis.
We have proposed a framework in which **gravity is not a force** acting within quantum mechanics but an **emergent geometric property** arising from the collapse of probabilistic futures into deterministic presents. Curvature corresponds to the local density of collapse events, and time emerges as the procedural measure of collapse progression. This unifies the probabilistic and deterministic descriptions of reality by separating their domains and connecting them through the **collapse mapping $C$**.
The implications are profound:
This picture replaces the search for a quantized spacetime with a deeper understanding: **spacetime itself is the history of collapse**, and **gravity is the self-consistent geometry** required to maintain that history.
To solidify the collapse mechanism, we integrate the **Relativistic Transactional Interpretation (RTI)** of quantum mechanics, as developed by Ruth E. Kastner (2022 book, with 2023 entropic gravity extensions). RTI provides a micro-relativistic process for collapse via transactions—unitary (U) evolution of offer/confirmation waves followed by non-unitary (NU) handshakes that actualize events. This bridges GAC's abstract \( C \) with dynamic "becoming," where **gravity emerges from entropic-geometric traces of transaction-collapse events**.
GAC's probabilistic future maps to RTI's quantum substratum (pre-transaction potentiae). The deterministic present emerges as RTI's causal set of actualized events. Collapse at \( \Sigma \) corresponds to RTI's lightlike handshake frontier.
**Step 1: Pre-Transaction State**: Superposition \( |\psi\rangle \) under Schrödinger evolution (U-interaction in RTI).
**Step 2: Trigger**: Interaction = emitter-absorber handshake; rate \( \Gamma_C = \frac{1}{\hbar} \frac{d}{dt} \langle \hat{H} \rangle \) as transaction probability.
**Step 3: Actualization**: NU-handshake realizes event; \( T_{\mu\nu}^{\text{(present)}} = C[\langle \hat{T}_{\mu\nu} \rangle] \), with direct-action fields.
**Step 4: Density**: \( \rho_C = \lambda_{\text{trans}} = \sum_i p_i^{\text{handshake}} \delta(x - x_i) \).
**Step 1: Transaction Density**: \( \rho_C = \lambda_{\text{trans}} \).
**Step 2: Entropic Bridge**: Entropy \( \bar{S} \propto \int \rho_C d^4x \); gradient \( \nabla S \propto \partial_\mu \rho_C \).
**Step 3: Curvature**: \( R = -8\pi G \rho_C \propto - \Delta S / vol \).
**Step 4: Newtonian Limit**: \( \nabla^2 \Phi = 4\pi G \kappa \lambda_{\text{trans}} \), with entropic \( \Phi = - (T / m) \Delta S \).
Transaction completion = collapse event: \( d\tau = k dC = k dN_{\text{trans}} \). \( \Sigma \) as causal set frontier.
\( P_{\text{QM}} \) as offer priors; \( \mathcal{L}_{\text{GR}} \) enforces handshake geometry.
In this extension, we derive an entropic component to the collapse-curva ture correspondence by integrating transactional elements from Schlatter & Kastner (2023), fulfilling Verlinde's entropic gravity program.
**Step 1: Transactional Entropy Generation**: Each transaction (handshake) in RTI increases local entropy by $\Delta S = k_B \ln(1/p_i)$, where $p_i$ is the confirmation probability of the handshake. The average entropy is given by $$ \bar{S} \propto \int \rho_C \, d^4x, $$ with the entropy gradient $$ \nabla S \propto \partial_\mu \rho_C, $$ linking the collapse density to entropic effects.
**Step 2: Linking to Curvature**: We insert the entropic gradient into the GAC curvature theorem. The Ricci scalar can be approximated as $$ R(x) = -8\pi G \rho_C(x) \approx - \frac{\nabla S}{T}, $$ where $T$ is the Unruh temperature associated with acceleration, derived from the rest-mass clocks in RTI as $T = \frac{\hbar a}{2\pi k_B c}$, with $a$ being the local acceleration.
**Step 3: Newtonian Limit with Entropy**: In the Newtonian limit, the gravitational potential $\Phi$ is related to the entropic gradient. We have $$ \Phi = - \frac{T}{m} \Delta S, $$ where $T = \frac{\hbar a}{2\pi k_B c}$ and $a \approx \frac{G M}{r^2}$ from classical gravity. This yields a potential consistent with Newtonian gravity at large scales, but introduces **MOND-like modifications** at low acceleration ($a \ll a_0$, where $a_0 \approx 1.2 \times 10^{-10} \, \text{m/s}^2$), and a **Cosmological Constant term from vacuum transaction entropy**, extending GAC without introducing new fields.
To address field-theoretic consistency, we now formulate the "**photographic collapse**" mechanism within a covariant quantum field framework. The goal is to show that **collapse can be represented as a local, stochastic *record field* that coexists with linear quantum dynamics, generating curvature** as the causal propagation of realized events.
Let ℋ be the Fock space of a real scalar field \( \hat{\phi}(x) \) on spacetime \( (\mathcal{M}, g_{\mu\nu}) \):
The state \( \rho \) evolves linearly under standard QFT. Collapse does not alter this; instead, it introduces a classical tensor field that records realized outcomes.
Introduce a classical tensor field \( R_{\mu\nu}(x) \), the *imprint* or “photograph” of the realized event structure, sourced by the local expectation of the stress–energy tensor plus stochastic fluctuations:
The operator \( \mathcal{P}_{\mu\nu}{}^{\alpha\beta} \) selects the physically relevant part of the source: for gravitational-wave (vacuum) contexts it is taken as **transverse–traceless (TT)**; for matter or Newtonian limits it reduces to a **dust-like projection**.
The constant \( \mu \) sets the imprint’s inverse range. **Calibration:** \( \mu = m_P = \sqrt{\hbar c/G} \) matches the Planck-scale proportionality \( k = \sqrt{\hbar G / c^5} \) introduced in the time–collapse relation.
The fluctuation tensor \( \xi_{\mu\nu}(x) \) represents random confirmations of RTI transactions, modeled as a mean-zero Gaussian process with correlator
A convenient local and Lorentz-invariant form in flat spacetime is \( N_{\mu\nu\alpha\beta}(x,y) = \eta_{\mu(\alpha}\eta_{\beta)\nu}\,A_0\,\delta^{(4)}(x-y) \). On curved backgrounds this generalizes to the standard *bitensor* form used in general relativity:
Here \( \delta^{(4)}(x-y)/\sqrt{-g(x)} \) is the covariant scalar-density delta ensuring proper tensor weight. **Amplitude calibration.** In the RTI picture, \( A_0 \) encodes the local transaction intensity. Linking to Section 10.2’s collapse rate \( \Gamma_C \):
where \( \hat{\mathcal{H}}(x) \) is the Hamiltonian density and \( \alpha \) is a dimensionless calibration factor. Present mesoscopic-scale data (Section 8.1) suggest a plausible range \( 0.1 \lesssim \alpha \lesssim 10 \).
Spacetime curvature responds to both the quantum expectation and the classical record:
The trace \( \rho_C = g^{\mu\nu} R_{\mu\nu} \) defines the *collapse density*. Conservation holds in expectation, \( \nabla^\mu \mathbb{E}[T^{\text{eff}}_{\mu\nu}] = 0 \), satisfying the Bianchi identity without altering QFT dynamics. The Planck-scale imprint mass \( \mu = m_P \) yields a short-ranged Green function \( G_R \!\propto\! e^{-\mu\ell}/\ell \), damping long-distance tails and preventing runaway self-interaction— a built-in regulator consistent with the renormalization-limit breakdown.
In the weak-field, slow-motion regime, the 00-component of \( T^{\text{eff}}_{\mu\nu} \) dominates. Linearizing \( g_{00} \approx 1 + 2\Phi/c^2 \), the Einstein equation reduces to
Thus, the Newtonian potential \( \Phi \) arises from both the averaged quantum mass density and the stochastic collapse density. In the limit \( \rho_C \to 0 \), one recovers the standard Poisson equation; the additional term gives the measurable gravitational imprint of collapse events.
The quantum state evolution remains governed by a linear, completely positive master equation with local Lindblad operators \( L_a(x) \). Because \( R_{\mu\nu} \) depends only on local expectations and Gaussian noise, no superluminal signaling or nonlinear effects occur.
The stochastic kernel \( N \) may be derived from transactional entropy exchange, \( \Delta S = k_B \ln(1/p_i) \), providing a thermodynamic interpretation of collapse noise. This yields MOND-like entropic corrections in the Newtonian limit, consistent with Section 10.6 and the RTI/entropic extension.
Hence, **collapse and field theory coexist consistently**: the wavefunction continues to evolve linearly, while the realized “photographic” record \( R_{\mu\nu} \) propagates as the physical source of gravity and time.
Under a Lorentz-covariant stochastic collapse dynamics with a smeared mass operator, Gaussian noise, and a Planck-scale regulator, the system satisfies: (i) a linear, completely-positive master equation ensuring **no-signaling**, (ii) energy–momentum conservation on average, (iii) curvature coupling reproducing $ R \propto -\rho_C $ and the Newtonian limit, and (iv) empirical discriminability via BMV/QGEM tests. The notation aligns with the draft (collapse density $ \rho_C $, time–collapse rule, etc.).
Consider a globally hyperbolic spacetime $ (\mathcal{M}, g_{\mu\nu}) $. Define the smeared mass-density operator $ M_f(x) $ with a Gaussian kernel $ f_{r_C} $ (width $ r_C = l_P $, the Planck length):
Here, $ \hat{M}(y) $ is the mass-density operator, and the 4D integral over $ \sqrt{-g} $ ensures covariance, avoiding UV singularities with a **Planck-scale cutoff**.
Postulate a fully covariant CSL-type evolution:
This preserves unitarity in expectation, with nonlinearity confined to noise realizations (the “photographic” collapse). The wavefunction persists; **collapse propagates as a covariant record**.
Averaging the SDE yields a linear, completely-positive local Lindblad equation:
The 4D local density ensures **no spacelike signaling**, maintaining relativistic causality.
Define the local collapse intensity and density:
This matches $ \rho_C \equiv dC/d^4x $ as the “exposure rate,” covariant under spacetime transformations.
Define the effective matter tensor:
The trace yields:
Here, $ V^\mu $ accounts for stochastic flux, vanishing in static equilibrium (Section 3.2).
The stochastic tensor’s divergence is:
With this choice, $ \nabla^\mu \langle T^{\text{eff}}_{\mu\nu} \rangle = 0 $, ensuring the **Bianchi identity holds on average**, preserving covariance.
In the weak-field limit ($ g_{00} \approx -(1 + 2\Phi/c^2) $):
Calibrate $ \kappa $ from the collapse kernel (Section 3.1), setting $ \kappa \rho_C \to \rho $ in static conditions, recovering **Newtonian gravity**.
The expected tick rate along $ u^\mu $ is $ \mathbb{E}[dN] = \lambda u^\mu d\Sigma_\mu $. Thus:
With $ k = \sqrt{\hbar G / c^5} $ from inertial calibration (Section 4).
From the master equation, single-particle kinetic heating (Gaussian smearing $ r_C $) is:
Here, $ r_C = l_P $ (the Planck length) and $ \gamma \approx \hbar / (k_B T_{\text{Unruh}}) $ (with $ T_{\text{Unruh}} = \hbar a / (2\pi k_B c) $) tie to $ \mu = m_P $ and $ k $ for dimensional consistency. The condition $ \gamma r_C^2 \ll \hbar / m $ ensures that atomic and molecular systems remain effectively unheated.
Consider two masses \( m_1 \) and \( m_2 \) in spatial superposition states \( |\psi_1\rangle = (|0\rangle + |d\rangle)/\sqrt{2} \) and \( |\psi_2\rangle = (|0\rangle + |d\rangle)/\sqrt{2} \) (separation \( d \), evolution time \( \tau \)):
We propose an abstract extension to the **Transaction-Collapse Gravity (TCG) model**, framing **annihilation at the quantum level as both destruction and creation**: it annihilates quantum superpositions while pushing a "commit" to the GR domain, akin to a printing press imprinting deterministic reality from probabilistic ink. This duality aligns with GAC's collapse projection and RTI's handshake actualization, where **annihilation generates the light-speed projection of spacetime**.
Annihilation in the quantum domain is not mere destruction but a creative process: it cancels probabilistic duality (e.g., superposition states), committing a definite outcome to the GR domain. This "push" manifests as the emergent shadow of gravity, projecting spacetime at light speed. Metaphorically, it's a printing press: quantum potentiae as fluid ink, annihilation as the press strike, and GR as the printed page—both annihilating (erasing quantum ambiguity) and creating (imprinting deterministic geometry).
**Step 1: Quantum Domain Setup**
In the quantum domain (pre-collapse $\mathcal{H}$), states are superpositions
evolving unitarily (RTI U-interaction). Annihilation involves duality pairs (e.g., particle $\psi_+$ and antiparticle $\psi_-$ modes).
**Step 2: Annihilation at Boundary**
At $\Sigma$ (critical interface), $\psi_+ + \psi_- \rightarrow \gamma$ (lightlike boson), with amplitude $\langle\psi_+|\psi_-\rangle \sim |\zeta'(\rho_n)|^{-1}$ (analogous to zeta zero density for rate). This **annihilates quantum ambiguity** (dephasing superposition) while creating a commit: the boson $\gamma$ projects as null geodesic, sourcing gravity's shadow ($R \sim \nabla(\text{annihilation amplitude}) / \text{vol}$).
**Step 3: Creation in GR Domain**
The annihilation "pushes" to $\mathcal{M}$:
with $\rho_C \sim$ annihilation rate. In RTI, this mirrors handshake convergence; in GAC, procedural time $d\tau = k dC$ advances as "print cycle."
**Step 4: Integration with TCG**
Annihilation duality at $\Sigma$ enhances RTI handshake (annihilation as NU-actualization) and GAC collapse (creation as projection), consistent with entropic extension (annihilation entropy $\Delta S \sim k_B \ln(1/p_i)$ yielding MOND/Cosmological Constant).
The “Gravity as Collapse” (GAC) model carries implications far beyond the reconciliation of quantum mechanics and general relativity. It reframes not only the ontology of space, time, and gravity, but the nature of reality, information, and consciousness itself. The following themes outline the broader philosophical and physical significance of this framework.
In summary, if the Gravity–as–Collapse framework is correct, it not only resolves the rift between quantum mechanics and general relativity, it transforms our understanding of reality itself. The universe is not a block of spacetime, nor a collection of independent entities, but a **participatory process of actualization**—a vast, ongoing act of creation in which every observer plays an active role.
*Having explored the broad philosophical implications of our model, we now return to a fundamental physical principle to demonstrate its internal consistency.* The first law of thermodynamics—that energy cannot be created or destroyed, only transformed—is a cornerstone of physics. In the context...
The first law of thermodynamics—that energy cannot be created or destroyed, only transformed—is a cornerstone of physics. In the context of the **Gravity-as-Collapse (GAC) framework** and its converged **Transaction-Collapse Model (TCM)**, this principle is not violated but is given a deeper, ontological interpretation. Conservation is reframed as a fundamental accounting rule that governs the transition of energy from the probabilistic quantum future to the deterministic relativistic present.
In the GAC/TCM ontology, the total energy of the universe is a constant, but it exists in two distinct states:
The collapse mapping \( C: \mathcal{H} \rightarrow \mathcal{M} \) is the process that **transforms** energy from its probabilistic form into its deterministic form. Crucially, this is not the *creation* of new energy, but the *actualization* of pre-existing potential.
The **conservation of energy** is upheld as a global constraint on the collapse process. The total probabilistic energy in \( \mathcal{H} \) is exactly equal to the total deterministic energy that can ever be actualized in \( \mathcal{M} \).
Each local collapse event conserves energy by converting a quantum potential \( \Delta E_{\text{quantum}} \) into a classical, geometric imprint \( \Delta T_{\mu\nu} \). The **effective stress-energy tensor** \( T^{\text{eff}}_{\mu\nu} \) is constructed to be covariantly conserved on average, \( \nabla^\mu \mathbb{E}[T^{\text{eff}}_{\mu\nu}] = 0 \), satisfying the Bianchi identity.
This conservation is a necessary condition for the self-consistency of the emergent spacetime. The "**bookkeeper**" role of gravity (Section 4.3) is precisely to enforce this balance. The curvature generated by a collapse event, \( R \propto -\rho_C \), is the **geometric ledger entry** that records the newly realized energy.
The model might seem to suggest that collapse "creates" the deterministic universe from nothing. However, the quantum domain \( \mathcal{H} \) is not "nothing"; it is a physically real, albeit probabilistic, substrate. The energy of the classical world is not created *ex nihilo* during collapse; it is **transferred** from the reservoir of quantum potential.
A useful analogy is a financial system with a fixed total money supply. Money can exist in a "potential" state or an "actual" state. A transaction (collapse) converts potential money into actual money. No new money is created in the system; it merely changes its state. The total money supply (total energy) is conserved.
This framework naturally **resolves the cosmological constant problem**. The vast zero-point energy of the quantum vacuum is part of the *probabilistic* energy budget. It is **unactualized potential and therefore does not gravitate**. It only contributes to spacetime curvature if it is actualized through a collapse process. The small, observed cosmological constant can then be interpreted as the entropic or stochastic imprint of a very low, persistent rate of vacuum-level collapse events (Section 10.6), a tiny but non-zero "transaction cost."
In summary, the principle that **energy cannot be created or destroyed is foundational** to the GAC/TCM framework. It is the guiding rule that connects the two ontological domains: the infinite potential of the quantum future and the finite, realized geometry of the relativistic present. Conservation of energy is the bridge across which reality is continuously built.
We present a concise formalism in which **quantum collapse is interpreted as the *reflection* of ubiquitous potential** across a quantum horizon, producing the finite, lightlike expression we observe as spacetime geometry. The quantum domain is treated as an unbounded substrate of potentiality; each interaction with this substrate generates a reflective output---a localized shard of realized potential---that propagates causally at the speed of light. Building on the annihilation--creation program, we reframe annihilation as reflective exchange rather than destruction: potential is mirrored into actuality, and the photon is the propagation of that reflective imprint. The expansion or compaction of the reflected collapse flow determines physical regimes: unimpeded flow yields vacuum, balanced null flow yields light, and compacted flow yields curvature and mass. **Observation is described as impedance** within this flow, locally blocking and reflecting potential to trigger collapse. Proper time emerges as the monotone of realized potential. This framework unifies vacuum, light, mass, gravity, and observation as distinct regimes of a single process: the reflective expression of infinite potential.
Quantum mechanics describes an unbounded manifold of possibilities, while general relativity describes a deterministic geometry of realized events. We adopt the view that the quantum substrate is not ``elsewhere'' but ***ubiquitous***, acting as an **event horizon of potentiality** that mirrors interactions into realized outcomes. The act commonly termed ``annihilation'' is here reinterpreted as reflective exchange with this horizon, producing a finite expression that advances causally as a lightlike front. Our objective is to formalize (i) the mapping from potential to realized geometry, (ii) the role of potential gradients in triggering collapse, and (iii) the reflective relation that identifies **photons as the outward propagation of interaction imprints**.
Let $\mathcal{H}$ denote the probabilistic (potential) domain, and $\mathcal{M}$ the realized spacetime manifold with metric $g_{\mu\nu}$. A collapse/realization map
extracts localized shards of potential as realized events. Define the *collapse density* (realization intensity)
so **curvature is the geometric record of realized potential**. Proper time arises as the procedural monotone of realization,
such that **time advances only where collapse/realization occurs**.
**Realization propagates along a null *collapse front* $\Sigma$** separating unexpressed potential from realized geometry:
Light operationally coincides with this frontier: **it carries the imprint of realization at $c$**, consistent with the null character of $\Sigma$.
Let $C(x)$ be a scalar collapse potential whose gradients encode local *strain* toward realization. Define the gradient tensor and magnitude
Collapse triggers when the strain exceeds a critical slope $\Gamma_c$,
with regimes classified by gradient amplitude and structure:
| Regime | Condition | Interpretation |
|---|---|---|
| Vacuum | $|\nabla C|\approx 0$ | Minimal realization; collapse rare |
| Light (null front) | $|\nabla C|=\Gamma_c$ | Specular propagation at $c$ |
| Mass/matter | $|\nabla C|>\Gamma_c$ | Localized, persistent realization |
| Gravity/curvature | $\nabla^2 C\neq 0$ | Gradient discontinuity; curvature imprint |
Interactions between shards arise from overlapping gradients, introducing interference terms $\delta\Pi_{\mu\nu}=\partial_\mu C_1\,\partial_\nu C_2+\partial_\mu C_2\,\partial_\nu C_1$, which can flatten (radiate), sharpen (condense), or cancel (revert to vacuum) the local potential field.
In this picture, **vacuum and mass are temporal complements**. In vacuum regions,
so **vacuum behaves as *arbitrary time potential***: a dormant reservoir of unexpressed future, traversable without inducing collapse. Conversely, in massive regions
indicating **persistent conversion of potential into actuality (time condensation)** with a concomitant curvature record—gravity.
We model the quantum substrate as a ubiquitous ***event horizon of potentiality***---a **mirror interface** between probability and geometry. The process conventionally labeled annihilation is recast as **reflective exchange** with this horizon: potential is not destroyed but mirrored into realized form. Let $\Psi_{\text{in}}$ denote the incoming configuration of potential and $\Psi_{\text{out}}$ the realized outcome; then
with **reflection operator $\mathcal{R}$** acting at the horizon. The **photon** (or radiative mode) is the ***propagating reflection*** of the interaction imprint. If $\mathcal{A}(x)$ denotes the local interaction (annihilation) amplitude, we express
Thus, vacuum, light, and mass correspond to distinct **optical conditions at the quantum mirror**: transparency (no reflection), specular null reflection, and absorptive/diffuse re-emission, respectively.
In this reflective framework, **observation is not an external cause of collapse but a boundary condition that impedes the free flow of potential** $C(x)$. Let $j_C^\mu = \rho_C k^\mu$ denote the flux of realized potential. In unobserved regions, potential flow is divergence-free,
representing transparent propagation through the vacuum horizon. Observation introduces an **impedance term $\chi(x)$**, producing local reflection and collapse:
When $\chi(x)$ exceeds a critical threshold, the flow of $C$ is partially reflected across the quantum horizon, generating a realized shard of potential---a collapse event. This process parallels optical reflection at an impedance mismatch, with a reflection coefficient
where $Z_q$ characterizes the quantum substrate and $Z_o$ the observational interface. Thus, **measurement impedes potential flow** rather than destroying it, and collapse arises as the reflected expression of that interaction.
The macroscopic expressions of realized potential follow from the distribution of $\rho_C$:
| Collapse regime | Condition | Physical mode |
|---|---|---|
| Expanding flow | $\nabla_\mu \rho_C \approx 0$ | Vacuum / flat space |
| Balanced flow | moderate $\rho_C$ | Stable spacetime trajectories (null/light) |
| Compacted flow | $\rho_C \uparrow \uparrow$ | Mass / strong curvature |
| Blocked flow | $\partial_\mu \rho_C \to \infty$ | Gravitational wells |
**Conservation is preserved** in the realized domain via $\nabla_\mu T^{\mu\nu}=0$, while
summarizes the curvature--collapse correspondence.
This reflection-based collapse formalism unifies vacuum, light, mass, gravity, observation, and time as regimes of a single process: the expression of infinite potential across a quantum horizon. Observation impedes the free flow of potential, producing reflection and realized outcomes; **photons propagate these reflections**, linking the potential and realized domains. Empirically, the framework motivates searches for **collapse-synchronized gravitational or radiative correlations** in mesoscopic systems, and for entropic signatures of reflection-driven realization. Future work may couple this model to a stochastic ``record field'' preserving linear quantum dynamics while sourcing curvature, establishing a continuous link between observation, reflection, and geometry.
The potential--expression tensor $\Pi_{\mu\nu}=\partial_\mu C\,\partial_\nu C$ compactly links geometry to realized potential. A concise relation
encodes curvature as the gradient energy of realization. This ansatz reproduces $R\propto -\rho_C$ in appropriate limits and makes explicit the role of potential gradients in sourcing spacetime structure.
In the reflective-collapse framework, **time is not a universal parameter** or static geometric coordinate but a **local rate of potential realization**. Each region of the universe expresses the infinite quantum potential at its own characteristic velocity
which quantifies the local “speed of becoming”---how rapidly potential converts into realized actuality. Variations in $v_C$ across spacetime constitute the **fundamental origin of gravitational and temporal relativity**.
Integrating the realization velocity defines the accumulated temporal age of a trajectory,
so that **older regions correspond to larger $T(x)$**, having realized more potential. Each trajectory thus represents a distinct stream of time---a localized rhythm of reality's unfolding.
Two trajectories, emitter and observer, possess respective realization velocities $v_C^{(\mathrm{emit})}$ and $v_C^{(\mathrm{obs})}$. Since the frequency of any signal or interaction is proportional to its local rate of realization,
their comparison yields the observed **redshift relation**:
If the observer occupies a newer domain of time realization ($v_C^{(\mathrm{obs})} > v_C^{(\mathrm{emit})}$), the older trajectory appears lagged in phase and its light is redshifted. If both share equal realization velocity, no shift occurs; if the observer’s time is slower ($v_C^{(\mathrm{obs})} < v_C^{(\mathrm{emit})}$), the signal appears blueshifted.
Hence, **redshift quantifies not geometric expansion but the *relative age of time* ** between trajectories of realization. Older photons, representing slower or earlier realizations of potential, are observed from newer domains as diminished in frequency. Each worldline carries its own temporal rhythm, and redshift expresses their differential maturity:
the spectral imprint of differing rates of becoming across concurrent domains of time.
Because the quantum substrate is an infinite field of potentiality, **all temporal states exist concurrently as latent possibilities**. Collapse does not create time; it expresses particular regions of this potential as realized trajectories. Each worldline $C(x)$ constitutes a path through the time-potential manifold, sampling it at its local velocity $v_C$. Different values of $v_C$ correspond to different temporal phases of realization: slower regions embody older stages of time, while faster regions express newer ones. All such phases coexist within the same potential reservoir but are locally realized at distinct rates.
Formally, every spacetime point corresponds to some degree of realized potential,
so that past ($C \approx C_{\mathrm{min}}$), present (actively increasing $C$), and future ($C \approx C_{\mathrm{max}}$) are **concurrent aspects of the same underlying potential field**. The “present” is not a universal slice but the moving interface where potential becomes actual along each trajectory.
Thus, all stages of time are simultaneously active within the quantum substrate. Each observer experiences only the portion of potential currently being realized at their own velocity $v_C$, while other regions---older, younger, or unexpressed---remain concurrently extant as differing phases of the universal process of realization. Time is therefore both *relative* and ***concurrent***: **relative in its local rate of realization, concurrent in its global coexistence within the infinite potential**.
Within this manifold of realization, each worldline $C(x)$ defines a continuous sequence of realized events---a monotonic increase of expressed potential---constituting the **linear structure of time**,
experienced as the sequential order of moments along a single trajectory. However, because all regions of potential coexist and may realize at different velocities, there exists not one global timeline but a continuum of concurrent realization paths $\{C_i(x)\}$. These form the **lateral structure of time**, representing the coexistence of multiple, phase-shifted streams of becoming:
where each index $i$ labels a distinct trajectory of potential realization.
**Linear time** describes the local, sequential flow of realization along one thread, while **lateral time** describes the simultaneous presence of all such threads within the quantum potential. Interactions between trajectories---through reflection, entanglement, or gravitational coupling---represent intersections of lateral timelines, where differing realizations exchange information and locally synchronize.
Accordingly, the universe embodies both linear and lateral forms of temporality: linear as the perceived progression of experience, and lateral as the concurrent ensemble of all realized and unrealized trajectories. Spacetime geometry emerges as the composite pattern of these interwoven temporal threads within the infinite potential field.
Quantum experiments consistently demonstrate causal structures that cannot be embedded in classical spacetime:
These phenomena challenge the classical assumption that all physical processes can be mapped to a unique, linear temporal sequence.
The apparent causal ambiguities arise from applying classical spacetime concepts to a domain where **temporal ordering is not yet defined**. In the quantum substrate ($\mathcal{H}$), causal relationships exist as **coherent superpositions of potential orderings**:
$$\Psi = \sum_{\text{orderings}} c_{i} \Psi_{i}$$
where each $\Psi_{i}$ represents a consistent configuration of events, but the temporal relationships between configurations remain indefinite.
The mapping *C*: $\mathcal{H} \rightarrow \mathcal{M}$ resolves this causal indefiniteness by **selecting one consistent temporal ordering** from the quantum ensemble. This process:
We formalize this through a **causal coherence functional**:
$$\mathcal{D}[\alpha,\beta] = \mathrm{Tr}[ C_{\alpha} \rho C_{\beta}^{\dagger} ]$$
where $\alpha$, $\beta$ represent different causal histories. The vanishing of off-diagonal terms ($\mathcal{D}[\alpha,\beta] \approx 0$ for $\alpha \neq \beta$) marks the transition to classical causal definiteness at the **inflection manifold $\Sigma$**.
This framework makes testable predictions:
Causal interoperability naturally incorporates:
The appearance of "retrocausality" or "acausality" dissolves when we recognize that these concepts presume the very spacetime framework that emerges from the causal resolution process.
**Quantum mechanics does not describe objects *in* spacetime**, but rather the fundamental **relational logic** from which **spacetime and objects co-emerge**. The quantum state \(|\psi\rangle\) encodes a network of possible interactions and correlations—a "pre-geometric" domain where concepts like "where" and "when" are not yet defined. In this framework, the wavefunction \(\Psi\) is not a field *in* a background, but a structure of **pure potentiality** from which background and foreground mutually arise.
Phenomena such as entanglement and superposition are primary in this view: they represent the intrinsic, non-spatial relatedness of the quantum substrate. What appears as indeterminacy from a classical perspective is, in fact, the **simultaneous presence of multiple, coherent relational patterns** awaiting realization.
**Key Insight:** Quantum mechanics describes the foundational level of physical reality, where relations are fundamental and spacetime is a derived, emergent structure. The wavefunction \(\Psi\) encodes the rules for this emergence, and the collapse process \(C\) is the mechanism that selects and instantiates a specific set of consistent relations as classical events.
**Spacetime geometry is not a pre-existing stage**. It is the **causal and geometric structure that is dynamically formed by the network of realized quantum interactions**. Each act of observation or measurement is a "**realization event**" that resolves quantum potential into a definite outcome, and in doing so, contributes a local "stitch" to the fabric of spacetime.
The perceived geometry is, therefore, **perspectival**. Each local observer's trajectory is defined by their own unique sequence of realization events (\(d\tau = k\,dC\)). The comparison between different local rates of realization gives rise to the experience of relative motion, time dilation, and gravitational potential. In this sense, **geometry is the view from inside the process**—the internal perspective of a system realizing itself through a web of interactions.
Within this ontology, the theory of General Relativity is revealed not as a fundamental description of reality, but as the **large-scale, emergent thermodynamics of the quantum realization process**.
The curvature of spacetime, described by Einstein's equations, does not directly reflect the presence of mass-energy, but rather the **local density and flow of realization events** (\(\rho_C\)). A region of high matter density is a region where quantum potential is being persistently and rapidly actualized. The resulting curvature (\(R \propto -\rho_C\)) is the geometric imprint of this high rate of actualization—the "stress" in the interactive fabric of the universe.
Thus, we can symbolically express:
**General Relativity is a subset of the thermodynamics** (\(\mathcal{T}\)) of Quantum Mechanics—it is the effective, coarse-grained description of how the collective process of quantum realization organizes itself into a consistent, classical geometry.
The **Converged Transaction-Collapse Model** culminates in a fundamental ontological claim: **the deterministic spacetime of General Relativity is the persistent geometry formed by realized quantum interactions.**
This framework posits a clean functional separation:
The transition between them is governed by the collapse map \(C\), which functions as a cosmic **resolution mechanism**:
This resolves central paradoxes by establishing that **only realized interactions gravitate**. The vast potential energy of the quantum vacuum, being unactualized, does not contribute to the cosmological constant. The gravitational field is not a force to be quantized, but the **geometric signature of the universe continuously resolving its quantum potential into classical fact.** The cosmos we inhabit is the dynamic, stable structure formed by this ongoing, participatory process of realization.
The Planck scale represents not a limit of smallness, but an ***ontological boundary*** where dimensional concepts undergo fundamental transformation:
This mathematical singularity marks the transition from dimensional spacetime to **non-dimensional potentiality**, where:
The divergences that appear in quantum field theory below Planck scale are not mathematical pathologies but *ontological boundary markers*:
Below the Planck boundary lies a domain characterized by:
The fundamental equation becomes:
Where Planck units serve as conversion factors between dimensional and non-dimensional domains.
This framework reveals that the quest to "quantize gravity" is misguided. Instead, we discover that:
**Spacetime geometry emerges through ontological inversion** where quantum potential transforms into geometric reality. This inversion represents a fundamental dimensional transformation - potentially a time inversion, energy inversion, topological inversion, or convective process - that bridges the quantum and classical domains:
This framework proposes:
The inversion is formalized as a **projective transformation**:
where \(\mathcal{H}_0\) represents zero-dimensional quantum potential, \(\mathcal{M}\) the emergent spacetime manifold, \(\rho_0\) primordial potential density, and \(\rho_C(x)\) local collapse density.
**Key Resolutions:**
Every spacetime point maintains connection to the zero-point via collapse mapping \(C\), making the universe a **holographic projection** from fundamental potential.
The collapse mapping \(C: \mathcal{H} \rightarrow \mathcal{M}\) operates with a **fundamental conversion rate** given by Einstein's equation:
This reformulation reveals that \(E = mc^2\) is not merely an energy-mass equivalence, but the ***exchange rate of the collapse process itself***. The constant \(c^2\) quantifies how much geometric mass emerges from each unit of quantum energy realized through collapse.
In this view, the **speed of light squared (\(c^2\)) becomes the fundamental conversion constant** between the probabilistic and deterministic domains - the "exchange rate" at the quantum-geometric interface.
**BMV/QGEM Entanglement Tests:** Our model predicts **no gravitational entanglement ($\phi = 0$)** prior to collapse, versus standard quantum gravity predictions of $\phi \approx G m^2\tau/\hbar d$. For $m = 10^{-14}$ kg, $d = 100$ $\mu$m, $\tau = 1$ s, **any measured phase > 0.1 radians falsifies our framework**.
**Collapse-Synchronized Gravity:** Predict **correlated gravitational fluctuations $\delta g \approx 10^{-14}$ m/s² timing-locked to collapse events** in mesoscopic systems ($m \sim 10^{-12}$ kg). Null result with 5$\sigma$ confidence would challenge the model.
**Heating Bounds:** Additional heating $dE/dt = 3\hbar^2\gamma/4m r_C^2 < 10^{-28}$ W for ultracold systems provides parameter constraints.